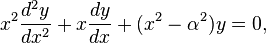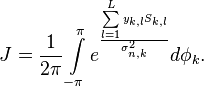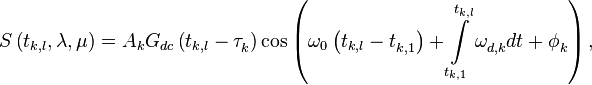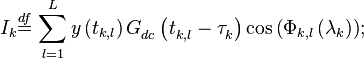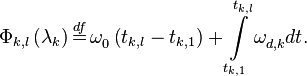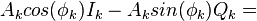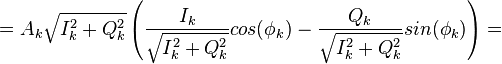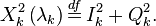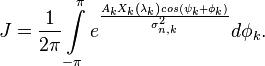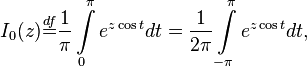Функции Бесселя — различия между версиями

Материал из SRNS
Перейти к: навигация, поиск
(→‎Модифицированные функции Бесселя первого рода при синтезе некогерентных систем)
(→‎Модифицированные функции Бесселя первого рода при синтезе некогерентных систем)
 
(не показаны 3 промежуточные версии 1 участника)
Строка 11: Строка 11:
  
 
Первого рода:
 
Первого рода:
−
<math>I_n(z)=\frac{1}{\pi}\int_0^\pi e^{z\cos t}\cos (nt)dt, \qquad n \in \mathbb Z, Re(z)>0.</math>
+
<math>I_n(z)=\frac{1}{\pi}\int\limits_0^\pi e^{z\cos t}\cos (nt)dt, \qquad n \in \mathbb Z, Re(z)>0.</math>
  
  
 
=== Модифицированные функции Бесселя первого рода при синтезе некогерентных систем ===
 
=== Модифицированные функции Бесселя первого рода при синтезе некогерентных систем ===
  
−
Исходный материал в исполнении Александра Ивановича доступен [[Media:20110416_Функция_Бесселя.doc|тут]].
+
Исходный материал в исполнении Александра Ивановича доступен в форматах [[Media:20110416_Функция_Бесселя.doc|doc]] и [[Media:20110416_Функция_Бесселя.pdf|pdf]].
  
 
При статистическом синтезе радиосистем в случаях, когда начальную фазу сигнала относят к неинформативным параметрам, возникает задача преобразования интеграла вида:
 
При статистическом синтезе радиосистем в случаях, когда начальную фазу сигнала относят к неинформативным параметрам, возникает задача преобразования интеграла вида:
−
<math>J = \frac{1}{2\pi}\int_{-\pi}^\pi e^{\frac{\sum\limits_{l=1}^L y_{k,l}S_{k,l}}{\sigma_{n,k}^2}} d\phi_k.</math>
+
:<math>J = \frac{1}{2\pi}\int\limits_{-\pi}^\pi e^{\frac{\sum\limits_{l=1}^L y_{k,l}S_{k,l}}{\sigma_{n,k}^2}} d\phi_k.</math>
  
 
Рассмотрим подробнее числитель экспоненты для типичной модели сигнала
 
Рассмотрим подробнее числитель экспоненты для типичной модели сигнала
−
<math>S\left( {{t}_{k,l}},\mathbf{\lambda },\mathbf{\mu } \right)=A_{k}{G}_{dc}\left( {{t}_{k,l}}-\tau _{k}^{{}} \right)\cos \left( {{\omega }_{0}}\left( {{t}_{k,l}}-t_{k,1}^{{}} \right)+\int\limits_{{{t}_{k,1}}}^{{{t}_{k,l}}}{\omega _{d,k}^{{}}dt}+\varphi _{k}^{{}} \right),</math>
+
:<math>S\left( {{t}_{k,l}},\mathbf{\lambda },\mathbf{\mu } \right)=A_{k}{G}_{dc}\left( {{t}_{k,l}}-\tau _{k}^{{}} \right)\cos \left( {{\omega }_{0}}\left( {{t}_{k,l}}-t_{k,1}^{{}} \right)+\int\limits_{{{t}_{k,1}}}^{{{t}_{k,l}}}{\omega _{d,k}^{{}}dt}+\phi _{k}^{{}} \right),</math>
  
 
тогда  
 
тогда  
 
        
 
        
−
<math>\sum_{l=1}^L y_{k,l}S_{k,l} = A_{k}cos(\phi_k){I}_{k} - A_{k}sin(\phi_k){Q}_{k},</math>
+
:<math>\sum_{l=1}^L y_{k,l}S_{k,l} = A_{k}cos(\phi_k){I}_{k} - A_{k}sin(\phi_k){Q}_{k},</math>
  
 
где  
 
где  
  
−
<math>{{I}_{k}}\overset{df}{\mathop{=}}\,\sum\limits_{l=1}^{L}{y\left( {{t}_{k,l}} \right)G_{dc}^{{}}\left( t_{k,l}^{{}}-\tau _{k}^{{}} \right)\cos \left( {{\Phi }_{k,l}}\left( {{\mathbf{\lambda }}_{k}} \right) \right)};</math>
+
:<math>{{I}_{k}}\overset{df}{\mathop{=}}\,\sum\limits_{l=1}^{L}{y\left( {{t}_{k,l}} \right)G_{dc}^{{}}\left( t_{k,l}^{{}}-\tau _{k}^{{}} \right)\cos \left( {{\Phi }_{k,l}}\left( {{\mathbf{\lambda }}_{k}} \right) \right)};</math>
  
−
<math>{{Q}_{k}}\overset{df}{\mathop{=}}\,\sum\limits_{l=1}^{L}{y\left( {{t}_{k,l}} \right)G_{dc}^{{}}\left( t_{k,l}^{{}}-\tau _{k}^{{}} \right)\sin \left( {{\Phi }_{k,l}}\left( {{\mathbf{\lambda }}_{k}} \right) \right)},</math>
+
:<math>{{Q}_{k}}\overset{df}{\mathop{=}}\,\sum\limits_{l=1}^{L}{y\left( {{t}_{k,l}} \right)G_{dc}^{{}}\left( t_{k,l}^{{}}-\tau _{k}^{{}} \right)\sin \left( {{\Phi }_{k,l}}\left( {{\mathbf{\lambda }}_{k}} \right) \right)},</math>
  
 
в которых
 
в которых
  
−
<math>{{\Phi }_{k,l}}\left( {{\mathbf{\lambda }}_{k}} \right)\overset{df}{\mathop{=}}\,\omega _{0}^{{}}\left( {{t}_{k,l}}-{{t}_{k,1}} \right)+\int\limits_{{{t}_{k,1}}}^{{{t}_{k,l}}}{\omega _{d,k}^{{}}dt}.</math>
+
:<math>{{\Phi }_{k,l}}\left( {{\mathbf{\lambda }}_{k}} \right)\overset{df}{\mathop{=}}\,\omega _{0}^{{}}\left( {{t}_{k,l}}-{{t}_{k,1}} \right)+\int\limits_{{{t}_{k,1}}}^{{{t}_{k,l}}}{\omega _{d,k}^{{}}dt}.</math>
  
  
−
Далее производится красивый хак: очевидно, что <math>\forall I_k, Q_k \in \R {\ }: \exists \psi_k\in \R</math>, такая что:
+
Далее производится красивый хак: очевидно, что <math>\forall I_k, Q_k \in \R {\ }: \exists \psi_k\in \R</math>, такое что:
  
−
<math>\!\! A_{k} cos(\phi_k){I}_{k} - A_{k}sin(\phi_k){Q}_{k} = \!\!</math>
+
:<math>\!\! A_{k} cos(\phi_k){I}_{k} - A_{k}sin(\phi_k){Q}_{k} = \!\!</math>
−
<math>A_{k} \sqrt{I_k^2 + Q_k^2} \left(
+
:<math>=A_{k} \sqrt{I_k^2 + Q_k^2} \left(
 
\frac{I_k}{\sqrt{I_k^2 + Q_k^2}} cos(\phi_k) -
 
\frac{I_k}{\sqrt{I_k^2 + Q_k^2}} cos(\phi_k) -
 
\frac{Q_k}{\sqrt{I_k^2 + Q_k^2}} sin(\phi_k) \right) = </math>
 
\frac{Q_k}{\sqrt{I_k^2 + Q_k^2}} sin(\phi_k) \right) = </math>
−
<math>A_{k} \sqrt{I_k^2 + Q_k^2} \left( cos(\psi_k) cos(\phi_k){I}_{k} - A_{k}sin(\psi_k)sin(\phi_k) \right)=</math>
+
:<math>=A_{k} \sqrt{I_k^2 + Q_k^2} \left( cos(\psi_k) cos(\phi_k) - sin(\psi_k)sin(\phi_k) \right)=
−
<math>A_{k} X_{k}\left( {{\mathbf{\lambda }}_{k}} \right) cos(\psi_k + \phi_k),</math>
+
A_{k} X_{k}\left( {{\mathbf{\lambda }}_{k}} \right) cos(\psi_k + \phi_k),</math>
  
 
где  
 
где  
−
<math>X_{k}^{2}\left( {{\mathbf{\lambda }}_{k}} \right)\overset{df}{\mathop{=}}\,I_{k}^{2}+Q_{k}^{2}.</math>  
+
:<math>X_{k}^{2}\left( {{\mathbf{\lambda }}_{k}} \right)\overset{df}{\mathop{=}}\,I_{k}^{2}+Q_{k}^{2}.</math>  
  
  
 
С учетом проделанных преобразованием, можно записать:
 
С учетом проделанных преобразованием, можно записать:
−
<math>J = \frac{1}{2\pi}\int_{-\pi}^\pi e^{\frac{A_{k} X_{k}\left( {{\mathbf{\lambda }}_{k}} \right) cos(\psi_k + \phi_k)}{\sigma_{n,k}^2}} d\phi_k.</math>
+
:<math>J = \frac{1}{2\pi}\int\limits_{-\pi}^\pi e^{\frac{A_{k} X_{k}\left( {{\mathbf{\lambda }}_{k}} \right) cos(\psi_k + \phi_k)}{\sigma_{n,k}^2}} d\phi_k.</math>
  
  
 
По определению, модифицированная функция Бесселя первого рода нулевого порядка:
 
По определению, модифицированная функция Бесселя первого рода нулевого порядка:
−
<math>I_0(z)\overset{df}{\mathop{=}}\frac{1}{\pi}\int_0^\pi e^{z\cos t}dt = \frac{1}{2\pi}\int_{-\pi}^\pi e^{z\cos t}dt,</math>
+
:<math>I_0(z)\overset{df}{\mathop{=}}\frac{1}{\pi}\int\limits_0^\pi e^{z\cos t}dt = \frac{1}{2\pi}\int\limits_{-\pi}^\pi e^{z\cos t}dt,</math>
  
 
тогда с учетом того, что подынтегральная функция в полученном выражении для <math>\!\! J </math> периодична и её период совпадает с периодом интегрирования, а значит замена аргумента <math>\!\! \phi_k </math> на <math>\!\! \phi_k + \psi_k </math> не меняет значения интеграла, получаем выражение:
 
тогда с учетом того, что подынтегральная функция в полученном выражении для <math>\!\! J </math> периодична и её период совпадает с периодом интегрирования, а значит замена аргумента <math>\!\! \phi_k </math> на <math>\!\! \phi_k + \psi_k </math> не меняет значения интеграла, получаем выражение:
−
<math>J = I_0 \left( \frac{A_{k} X_{k}\left( {{\mathbf{\lambda }}_{k}} \right)}{\sigma_{n,k}^2} \right).</math>
+
:<math>J = I_0 \left( \frac{A_{k} X_{k}\left( {{\mathbf{\lambda }}_{k}} \right)}{\sigma_{n,k}^2} \right).</math>
 +
 
 +
== См. также ==
 +
[http://ru.wikipedia.org/wiki/Модифицированные_функции_Бесселя Модифицированные функции Бесселя] <br />
 +
[http://ru.wikipedia.org/wiki/Функции_Бесселя Функции Бесселя] <br />
  
 
[[Категория:Статистическая радиотехника]]
 
[[Категория:Статистическая радиотехника]]

Текущая версия на 10:44, 9 апреля 2012

Функции Бесселя в математике — семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя:

x^2 \frac{d^2 y}{dx^2} + x \frac{dy}{dx} + (x^2 - \alpha^2)y = 0,

где \alpha — произвольное вещественное число, называемое порядком.


[править] Модифицированные функции Бесселя

Модифици́рованные фу́нкции Бе́сселя — это функции Бесселя от чисто мнимого аргумента.

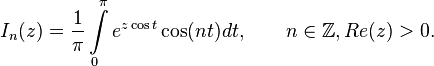
Первого рода: I_n(z)=\frac{1}{\pi}\int\limits_0^\pi e^{z\cos t}\cos (nt)dt, \qquad n \in \mathbb Z, Re(z)>0.


[править] Модифицированные функции Бесселя первого рода при синтезе некогерентных систем

Исходный материал в исполнении Александра Ивановича доступен в форматах doc и pdf.

При статистическом синтезе радиосистем в случаях, когда начальную фазу сигнала относят к неинформативным параметрам, возникает задача преобразования интеграла вида:

J = \frac{1}{2\pi}\int\limits_{-\pi}^\pi e^{\frac{\sum\limits_{l=1}^L y_{k,l}S_{k,l}}{\sigma_{n,k}^2}} d\phi_k.

Рассмотрим подробнее числитель экспоненты для типичной модели сигнала

S\left( {{t}_{k,l}},\mathbf{\lambda },\mathbf{\mu } \right)=A_{k}{G}_{dc}\left( {{t}_{k,l}}-\tau _{k}^{{}} \right)\cos \left( {{\omega }_{0}}\left( {{t}_{k,l}}-t_{k,1}^{{}} \right)+\int\limits_{{{t}_{k,1}}}^{{{t}_{k,l}}}{\omega _{d,k}^{{}}dt}+\phi _{k}^{{}} \right),

тогда

\sum_{l=1}^L y_{k,l}S_{k,l} = A_{k}cos(\phi_k){I}_{k} - A_{k}sin(\phi_k){Q}_{k},

где

{{I}_{k}}\overset{df}{\mathop{=}}\,\sum\limits_{l=1}^{L}{y\left( {{t}_{k,l}} \right)G_{dc}^{{}}\left( t_{k,l}^{{}}-\tau _{k}^{{}} \right)\cos \left( {{\Phi }_{k,l}}\left( {{\mathbf{\lambda }}_{k}} \right) \right)};
{{Q}_{k}}\overset{df}{\mathop{=}}\,\sum\limits_{l=1}^{L}{y\left( {{t}_{k,l}} \right)G_{dc}^{{}}\left( t_{k,l}^{{}}-\tau _{k}^{{}} \right)\sin \left( {{\Phi }_{k,l}}\left( {{\mathbf{\lambda }}_{k}} \right) \right)},

в которых

{{\Phi }_{k,l}}\left( {{\mathbf{\lambda }}_{k}} \right)\overset{df}{\mathop{=}}\,\omega _{0}^{{}}\left( {{t}_{k,l}}-{{t}_{k,1}} \right)+\int\limits_{{{t}_{k,1}}}^{{{t}_{k,l}}}{\omega _{d,k}^{{}}dt}.


Далее производится красивый хак: очевидно, что 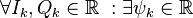\forall I_k, Q_k \in \R {\ }: \exists \psi_k\in \R, такое что:

\!\! A_{k} cos(\phi_k){I}_{k} - A_{k}sin(\phi_k){Q}_{k} = \!\!
=A_{k} \sqrt{I_k^2 + Q_k^2} \left( \frac{I_k}{\sqrt{I_k^2 + Q_k^2}} cos(\phi_k) - \frac{Q_k}{\sqrt{I_k^2 + Q_k^2}} sin(\phi_k) \right) =
=A_{k} \sqrt{I_k^2 + Q_k^2} \left( cos(\psi_k) cos(\phi_k) - sin(\psi_k)sin(\phi_k) \right)= A_{k} X_{k}\left( {{\mathbf{\lambda }}_{k}} \right) cos(\psi_k + \phi_k),

где

X_{k}^{2}\left( {{\mathbf{\lambda }}_{k}} \right)\overset{df}{\mathop{=}}\,I_{k}^{2}+Q_{k}^{2}.


С учетом проделанных преобразованием, можно записать:

J = \frac{1}{2\pi}\int\limits_{-\pi}^\pi e^{\frac{A_{k} X_{k}\left( {{\mathbf{\lambda }}_{k}} \right) cos(\psi_k + \phi_k)}{\sigma_{n,k}^2}} d\phi_k.


По определению, модифицированная функция Бесселя первого рода нулевого порядка:

I_0(z)\overset{df}{\mathop{=}}\frac{1}{\pi}\int\limits_0^\pi e^{z\cos t}dt = \frac{1}{2\pi}\int\limits_{-\pi}^\pi e^{z\cos t}dt,

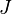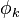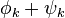тогда с учетом того, что подынтегральная функция в полученном выражении для \!\! J периодична и её период совпадает с периодом интегрирования, а значит замена аргумента \!\! \phi_k на \!\! \phi_k + \psi_k не меняет значения интеграла, получаем выражение:

J = I_0 \left( \frac{A_{k} X_{k}\left( {{\mathbf{\lambda }}_{k}} \right)}{\sigma_{n,k}^2} \right).

[править] См. также

Модифицированные функции Бесселя
Функции Бесселя

Источник — «https://blog.srns.ru/index.php?title=Функции_Бесселя&oldid=6228»
Персональные инструменты
Пространства имён

Варианты
Действия
SRNS Wiki
Рабочие журналы
Приватный файлсервер
QNAP Сервер
Инструменты