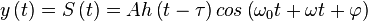Задание 7 к практическим занятиям (ММ РУиС) — различия между версиями
Материал из SRNS
Korogodin (обсуждение | вклад) (Новая страница: «'''Тема занятия:''' Статистический эквивалент коррелятора '''Цели занятия:''' * убедиться в р…») |
Korogodin (обсуждение | вклад) (→Задача 7.1) |
||
| Строка 11: | Строка 11: | ||
Построить зависимости выходных сигналов коррелятора от ошибки по задержке <math>\delta\tau</math>, частоте <math>\delta\omega</math> и фазе <math>\delta\varphi</math> при воздействии полезного сигнала в отсутствии шумов | Построить зависимости выходных сигналов коррелятора от ошибки по задержке <math>\delta\tau</math>, частоте <math>\delta\omega</math> и фазе <math>\delta\varphi</math> при воздействии полезного сигнала в отсутствии шумов | ||
:<math>y\left(t\right) = S\left(t\right) = A h\left(t - \tau\right) cos\left(\omega_0t + \omega t + \varphi\right)</math> | :<math>y\left(t\right) = S\left(t\right) = A h\left(t - \tau\right) cos\left(\omega_0t + \omega t + \varphi\right)</math> | ||
| − | и сравнить результаты с аналогичными для статистических эквивалентов. | + | и сравнить результаты с аналогичными для статистических эквивалентов. <math>h\left(t\right)</math> - функция модуляции псевдослучайной последовательностью. |
'''Комментарии''': | '''Комментарии''': | ||
Версия 18:31, 1 мая 2014
Тема занятия: Статистический эквивалент коррелятора Цели занятия:
- убедиться в работоспособности статистических эквивалентов коррелятора;
- развить навыки моделирования сигналов со случайными параметрами;
- развить навыки обработки результатов статистических экспериментов.
Задача 7.1
Постановка задачи:
Построить зависимости выходных сигналов коррелятора от ошибки по задержке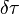 
, частоте 
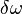и фазе 
при воздействии полезного сигнала в отсутствии шумов
и сравнить результаты с аналогичными для статистических эквивалентов.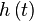 
- функция модуляции псевдослучайной последовательностью.
Комментарии:
1) В ходе практического занятия рекомендуется использовать презентацию к лекции 11.
2) Пример формирования ФМ-2 сигнала:
Fd = 44.2e6/4; Td = 1/Fd;
tmax = 0.001; t = 0:Td:tmax;
N_PRN = 511; T_PRN = 0.001;
PRN = sign(randn(1, N_PRN));
ind_h = fix(mod(t/T_PRN, 1)*N_PRN) + 1;
h = PRN(ind_h);
A = 2;
f0 = 3e6;
phi = pi/4;
u = A * h .* cos(2*pi*f0*t + phi);
tmax = 0.001; t = 0:Td:tmax;
N_PRN = 511; T_PRN = 0.001;
PRN = sign(randn(1, N_PRN));
ind_h = fix(mod(t/T_PRN, 1)*N_PRN) + 1;
h = PRN(ind_h);
A = 2;
f0 = 3e6;
phi = pi/4;
u = A * h .* cos(2*pi*f0*t + phi);
