04.06.2011, Лабораторная работа по многолучевости
Korogodin (обсуждение | вклад) (→Домашняя подготовка) |
Korogodin (обсуждение | вклад) |
||
| Строка 5: | Строка 5: | ||
| − | + | <center>'''Моделирование многолучевого распространения сигнала СРНС в среде Matlab'''</center> | |
== Введение == | == Введение == | ||
Версия 20:06, 4 июня 2011
<accesscontrol>SuperUsers</accesscontrol>
Задача: разработать методическое пособие и отработать выполнение лабораторной работы по многолучевому распространению сигналов СРНС на основе модели.
За образец оформления и стиля предлагается взять методическое пособие "МОДЕЛИРОВАНИЕ УСТРОЙСТВ ОБРАБОТКИ СИГНАЛОВ В ПРОГРАММЕ SYSTEM VIEW. Лабораторная работа № 3" авторства Сизяковой А.Ю.
Содержание
|
Введение
Спутниковые навигационные системы и их приложения в современном мире играют огромную роль: они способствуют развитию экономики страны, улучшают условия жизни людей, укрепляют оборону страны. Развитие навигационных технологий не останавливается: совершенствуются и космический, и наземный, и потребительский сегменты. Одна из существующих задач – повышение точности навигационных определений, одна из существующих проблем на этом пути – многолучевое распространение сигналов. Данная проблема особо остро стоит при применении навигационной аппаратуры потребителей (НАП) в условиях городской застройки, в составе военных комплексов (бронетехника, суда), при высокоточных фазовых измерениях.
Для борьбы с влиянием многолучевого распространения необходимо изучить характер этого влияния. Антенну, фронтенд и корреляторы навигационного приемника можно считать, в некотором приближении, линейными устройствами. Прохождение через них навигационного сигнала хорошо изучено. Для составления адекватной модели процессов в этих элементах приемника достаточно определить запаздывание, ослабление и фазовый сдвиг отраженного сигнала относительно прямого. Тогда в качестве модели процессов можно принять суперпозицию откликов на прямой и отраженный сигнал.
В настоящей лабораторной работе студентам предлагается развить свои представления о многолучевом распространении сигнала и его влиянии на приемник на предельно простом, но практически ценном модельном примере: приеме сигналов неподвижным приемником в условиях переотражения от вертикального экрана конечных размеров, расположенном на некотором расстоянии от приемной антенны.
Лабораторный практикум включает в себя:
- ознакомление с математической моделью многолучевого распространения и его воздействия на навигационный приемник;
- самостоятельный численный расчет отдельных зависимостей с помощью приведенной математической модели;
- моделирование многолучевого распространения сигнала СРНС в программе, созданной в среде Matlab;
- обработку и сравнение полученных результатов.
Модель многолучевого распространения сигналов и его влияния на сигналы на выходе коррелятора
Проведем логические рассуждения, на основе которых получим математические модели многолучевого распространения и сигналов коррелятора.
Исходные данные
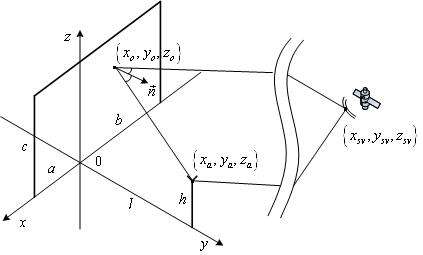
Опишем Землю, отражающий экран, фазовый центр антенны навигационного спутника и фазовый центр приемной антенны НАП как сферу, ограниченный прямоугольником участок плоскости и две точки в трехмерном пространстве соответственно (см. рисунок 1).
Для этого зададим две декартовы системы координат:
- СК
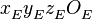 , связанная с центом Земли (сферы);
, связанная с центом Земли (сферы);
- СК
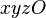 , связанная с СК преобразованием:
, связанная с СК преобразованием:
 , (1)
, (1)
- где - средний радиус Земли, равный 6 371 км.
Пусть, известна высота экрана 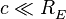 и его ширина
и его ширина 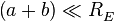 . Тогда, в СК
. Тогда, в СК 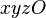 плоскость отражающего экрана описывается уравнением
плоскость отражающего экрана описывается уравнением 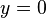 , а его точки удовлетворяют соотношениям:
, а его точки удовлетворяют соотношениям:
 (2)
(2)
Пусть, на некотором расстоянии 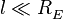 от экрана, значительно меньшем радиуса Земли, расположена приемная антенна, поднятая над поверхностью на высоту
от экрана, значительно меньшем радиуса Земли, расположена приемная антенна, поднятая над поверхностью на высоту 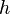 . Тогда, в качестве модели фазового центра антенны в СК
. Тогда, в качестве модели фазового центра антенны в СК 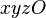 выступает точка
выступает точка  или её радиус-вектор
или её радиус-вектор 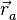 , где
, где
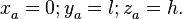 (3)
(3)
Моделью фазового центра передающей антенны спутника выступает точка 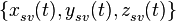 (или её радиус-вектор
(или её радиус-вектор 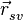 ), движущаяся вокруг центра СК
), движущаяся вокруг центра СК 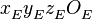 по соответствующему закону.
по соответствующему закону.
Если существует переотражённый от экрана сигнал, то точка его отражения имеет координаты 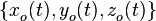 (радиус-вектор
(радиус-вектор 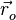 ).
).
Центр сферы расположен в точке 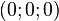 в СК
в СК 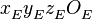 , радиус сферы -
, радиус сферы - 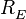 .
.
Рассматриваемая модель рассматривает отражение сигнала только от вертикального экрана. Сигналы, отражённые от поверхности земли, достаточно хорошо подавляются специализированными антеннами.
Модель многолучевого распространения
Поиск координат точки отражения
Примем гипотезу зеркального отражения от экрана. Тогда, угол падения сигнала равен углу его отражения:
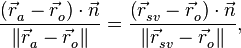 (4)
(4)
- где
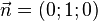 - вектор нормали к экрану.
- вектор нормали к экрану.
Введем векторы
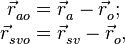 (5)
(5)
тогда выражение (4) преобразуется к виду
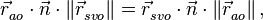 (6)
(6)
что в виду введенного определения 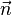 приводит к выражению
приводит к выражению
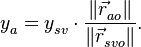 (7)
(7)
откуда следует
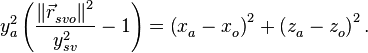 (8)
(8)
Нормаль, падающий луч и отраженный луч лежат в одной плоскости:
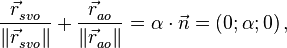 (9)
(9)
что для компонент x и z вырождается в выражения:
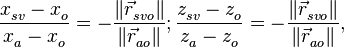 (10)
(10)
откуда
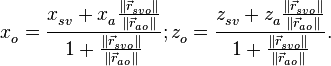 (11)
(11)
Воспользовавшись теоремой Пифагора для уравнения (8), получаем:
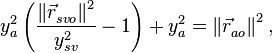
тогда
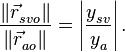 (13)
(13)
Подставляя выражение (13) в (11), получаем координаты точки отражения на бесконечном экране:
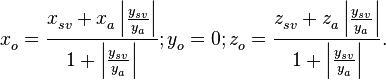 (14)
(14)
Условия наличия прямого и отраженного сигналов
Чтобы присутствовал отраженный сигнал, при просмотре из точки отражения спутник должен находиться над горизонтом и при этом выполняться неравенство 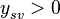 .
.
Определим условия видимости спутника из точки отражения (см. рисунок 2).
Тангенс угла места, под которым из точки отражения виден горизонт:
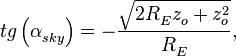 (15)
(15)
тангенс угла места, под которым спутник виден из точки отражения:
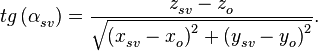 (16)
(16)
Условие нахождения спутника над горизонтом для точки отражения:
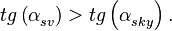 (17)
(17)
По аналогии найдем критерий наличия прямого сигнала. При возвышении спутника над горизонтом, при наблюдениях из точки фазового центра приемной антенны, выполняется неравенство:
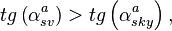 (18)
(18)
- где
 (19)
(19)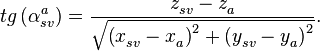 (20)
(20)
Когда спутник находится в полуплоскости 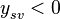 , его сигнал может быть затенен экраном. Точки прямой спутник – приемная антенна удовлетворяют уравнению:
, его сигнал может быть затенен экраном. Точки прямой спутник – приемная антенна удовлетворяют уравнению:
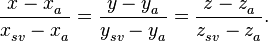 (21)
(21)
Тогда точка пересечения прямого луча с экраном имеет координаты:
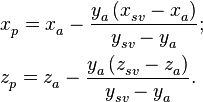 (22)
(22)
С учетом (2) получаем условие затенения экраном прямого сигнала спутника
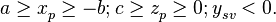 (23)
(23)
Тогда, для наличия прямого сигнала спутника должно выполняться соотношение (18) и не выполняться соотношения (23).
Координаты спутника
Опишем координаты спутника 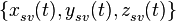 как функцию времени. Пусть, спутник движется по круговой орбите на высоте
как функцию времени. Пусть, спутник движется по круговой орбите на высоте 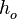 над средним уровнем Земли. Пусть, в начальный момент времени долгота восходящего узла составляет
над средним уровнем Земли. Пусть, в начальный момент времени долгота восходящего узла составляет 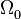 , наклонение орбиты
, наклонение орбиты 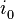 , угол начального положения на орбите
, угол начального положения на орбите 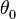 , тогда в СК
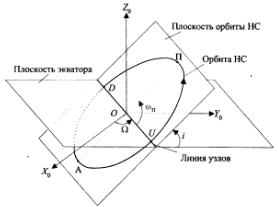
, тогда в СК 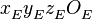 координаты спутника (см. рисунок 3) задаются выражением([1]):
координаты спутника (см. рисунок 3) задаются выражением([1]):
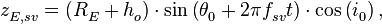 (24)
(24)
- где
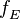 - частота вращения Земли (около
- частота вращения Земли (около 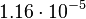 Гц),
Гц), 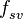 - частота вращения спутника (в зависимости от системы около
- частота вращения спутника (в зависимости от системы около 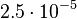 Гц). Переход от координат СК
Гц). Переход от координат СК 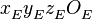 к координатам СК
к координатам СК 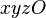 осуществляется с помощью преобразований (1).
осуществляется с помощью преобразований (1).
Разность хода прямого и отраженного лучей
Разность хода прямого и отраженного лучей можно после проведенных выкладок можно найти множеством способов, например прямым:
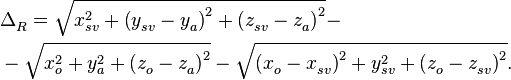 (25)
(25)
Модель выходного сигнала коррелятора при действии на входе приемника прямого и отраженного сигналов
Антенный модуль, фронтенд и коррелятор в отсутствии помех можно считать линейными устройствами. Тогда сигнал на выходе коррелятора при действии на входе антенны прямого и отраженного лучей можно представить как сумму реакций на прямой и отраженный сигнал.
При действии на выходе антенного модуля одного навигационного сигнала, выходной k-й отсчет коррелятора можно приближенно описать выражениями:
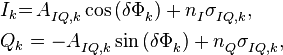 (26)
(26)
- где
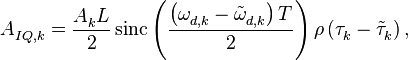 (27)
(27)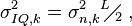 (28)
(28) (29)
(29)
- где
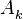 - амплитуда навигационного сигнала на входе АЦП,
- амплитуда навигационного сигнала на входе АЦП, 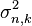 - дисперсия шума на входе АЦП,
- дисперсия шума на входе АЦП, 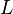 - число тактов АЦП участвующих в накоплении в корреляторе,
- число тактов АЦП участвующих в накоплении в корреляторе, 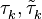 - задержка дальномерного кода сигнала спутника и опорного сигнала коррелятора,
- задержка дальномерного кода сигнала спутника и опорного сигнала коррелятора, 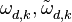 - циклическая частота сигнала спутника и опорного сигнала коррелятора,
- циклическая частота сигнала спутника и опорного сигнала коррелятора,  - начальная фаза навигационного сигнала на k-ом интервале,
- начальная фаза навигационного сигнала на k-ом интервале, 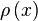 - корреляционная функция дальномерного кода,
- корреляционная функция дальномерного кода, 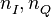 - некоррелированные белые гауссовские шумы.
- некоррелированные белые гауссовские шумы.
Темп изменения коэффициента отражения, угла прихода отраженного сигнала и т.п. значительно меньше темпа изменения фазовых соотношений между прямым и отраженным сигналом. Если не учитывать сдвиг фазы при отражении, фазовую характеристику антенны, сигнал на выходе коррелятора при многолучевом распространении можно описать выражениями
![\begin{align}
& {{I}_{k}}\overset{{}}{\mathop{=}}\,A_{IQ,k}^{{}}\left[ \cos \left( \delta \Phi _{k}^{{}} \right)+K_{MP,k}^{{}}\cos \left( \delta \Phi _{k}^{{}}+2\pi \frac{\Delta _{R,k}^{{}}}{\lambda } \right) \right]+n_{I}^{{}}\sigma _{IQ,k}^{{}}; \\
& {{Q}_{k}}=-A_{IQ,k}^{{}}\left[ \sin \left( \delta \Phi _{k}^{{}} \right)+K_{MP,k}^{{}}\sin \left( \delta \Phi _{k}^{{}}+2\pi \frac{\Delta _{R,k}^{{}}}{\lambda } \right) \right]+n_{Q}^{{}}\sigma _{IQ,k}^{{}}, \\
\end{align}](/images/math/1/8/1/181a0377e376a227e7dcbd00bc02a8e1.png) (30)
(30)
- где
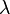 - длина волны несущей навигационного сигнала,
- длина волны несущей навигационного сигнала, 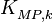 - коэффициент ослабления отраженного сигнала относительно прямого на выходе антенны.
- коэффициент ослабления отраженного сигнала относительно прямого на выходе антенны.
Для расчета коэффициента ослабления отраженного сигнала следует уточнить характер отражения от экрана и характеристики антенны.
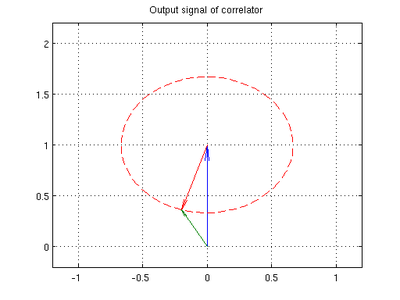
Модель выходного сигнала коррелятора (30) можно графически представить как сложение двух векторов комплексных сигналов – прямого и отраженного (см. рисунок 4).
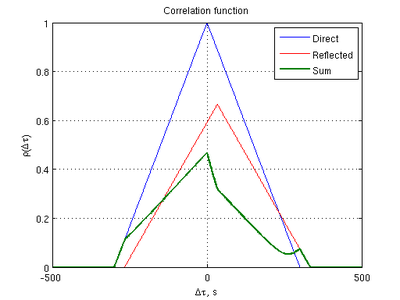
Воздействие отраженного сигнала приводит к фазовой и амплитудной модуляции суммарного сигнала - искажению корреляционной функции, меняющемуся во времени, см. рисунок 5.
Домашняя подготовка
Перед выполнением работ в лаборатории, обучающиеся проводят предварительную подготовку. Результаты студентами предоставляются индивидуально на бумажных носителях до начала выполнения лабораторного задания.
В процессе подготовки требуется:
- 1. Получить у преподавателя индивидуальную таблицу параметров.
- 2. Изучить математическую модель многолучевого распространения сигналов и процессов на выходе коррелятора.
- 3. Построить график зависимости высоты орбиты спутника
 для параметров, заданных в индивидуальной таблице. Занести результат в отчет.
для параметров, заданных в индивидуальной таблице. Занести результат в отчет.
- 3. Построить график зависимости высоты орбиты спутника
- 4. Для указанного момента времени определить разность хода прямого и отраженного лучей, ошибку, вносимую многолучевостью в фазу сигнала. Занести результат в отчет.
- 5. Подготовить ответы на контрольные вопросы.
Лабораторное задание
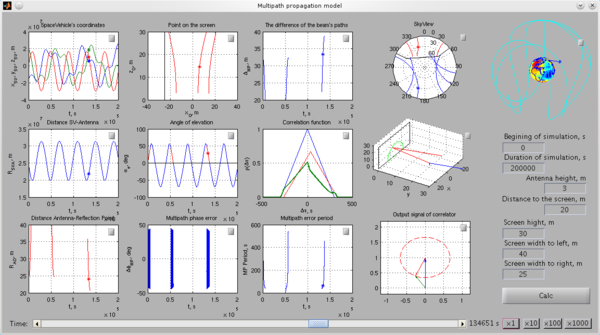
В лаборатории проводится моделирование многолучевого распространения сигнала с помощью программы, написанной в среде Matlab. Для выполнения скрипта следует запустить Matlab, перейти в соответствующую директорию и открыть файл main.m. Для запуска модели следует нажать клавишу клавиатуры F5 или кнопку Run (![]() ) в графическом интерфейсе Matlab'a, после чего открывается графический интерфейс программы (см. рисунок 6).
) в графическом интерфейсе Matlab'a, после чего открывается графический интерфейс программы (см. рисунок 6).

![\begin{align}
& x_{E,sv}^{{}}=\left( R_{E}^{{}}+h_{o}^{{}} \right)\cdot \left[ \cos \left( \theta _{0}^{{}}+2\pi f_{sv}^{{}}t \right)\cos \left( \Omega _{0}^{{}}+2\pi f_{E}^{{}}t \right) \right.- \\
& \begin{matrix}
{} & {} & {} & {} \\
\end{matrix}\left. -\sin \left( \theta _{0}^{{}}+2\pi f_{sv}^{{}}t \right)\sin \left( \Omega _{0}^{{}}+2\pi f_{E}^{{}}t \right)\cos \left( i_{0}^{{}} \right) \right], \\
\end{align}](/images/math/8/0/2/80249c6ef6a1ff0784fbcc13f8803c74.png)
![\begin{align}
& y_{E,sv}^{{}}=\left( R_{E}^{{}}+h_{o}^{{}} \right)\cdot \left[ \cos \left( \theta _{0}^{{}}+2\pi f_{sv}^{{}}t \right)\sin \left( \Omega _{0}^{{}}+2\pi f_{E}^{{}}t \right) \right.+ \\
& \begin{matrix}
{} & {} & {} & {} \\
\end{matrix}\left. +\sin \left( \theta _{0}^{{}}+2\pi f_{sv}^{{}}t \right)\cos \left( \Omega _{0}^{{}}+2\pi f_{E}^{{}}t \right)\cos \left( i_{0}^{{}} \right) \right], \\
\end{align}](/images/math/c/3/d/c3dbdff9b410fc3ba9f0e4280f754aae.png)
[ Хронологический вид ]Комментарии
Войдите, чтобы комментировать.