Моделирование коррелированных гауссовых СВ — различия между версиями
Материал из SRNS
Korogodin (обсуждение | вклад) (Новая страница: «При моделировании следящих систем НАП, а так же сигналов многоантенных НАП, возникает за…») |
Korogodin (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
При моделировании следящих систем НАП, а так же сигналов многоантенных НАП, возникает задача создания нормальных случайных величин с заданным коэффициентом корреляции. | При моделировании следящих систем НАП, а так же сигналов многоантенных НАП, возникает задача создания нормальных случайных величин с заданным коэффициентом корреляции. | ||
| − | == Многомерная нормальная СВ == | + | == Многомерная нормальная СВ или вектор случайных величин? == |
| − | + | При синтезе радиотехнических систем часто используются модели, оперирующие с многомерными нормальными распределениями. | |
| + | |||
| + | Определение из [http://ru.wikipedia.org/wiki/Многомерное_нормальное_распределение Википедии]: | ||
| + | Случайный вектор <math>\mathbf{X} = (X_1,\ldots, X_n)^{\top}: \Omega \to \mathbb{R}^n</math> имеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных условий: | ||
| + | |||
| + | * Произвольная линейная комбинация компонентов вектора <math>\sum\limits_{i=1}^n a_i X_i</math> имеет нормальное распределение или является константой. | ||
| + | * Существует вектор независимых стандартных нормальных случайных величин <math>\mathbf{Z}=(Z_1,\ldots, Z_m)^{\top}</math>, вещественный вектор <math>\mathbf{\mu} = (\mu_1,\ldots, \mu_n)^{\top}</math> и матрица <math>\mathbf{A}</math> размерности <math>n \times m</math>, такие что: | ||
| + | : <math>\mathbf{X} = \mathbf{A} \mathbf{Z} + \mathbf{\mu}</math>. | ||
| + | |||
| + | * Существует вектор <math>\mathbf{\mu} \in \mathbb{R}^n</math> и неотрицательно определённая симметричная матрица <math>\mathbf{\Sigma}</math> размерности <math>n \times n</math>, такие что характеристическая функция вектора <math>\mathbf{X}</math> имеет вид: | ||
| + | : <math>\phi_{\mathbf{X}}(\mathbf{u}) = e^{i \mathbf{\mu}^{\top} \mathbf{u} - \frac{1}{2}\mathbf{u}^{\top} \Sigma \mathbf{u}},\; \mathbf{u} \in \mathbb{R}^n</math>. | ||
[[Category:ММ РУиС (дисциплина)]] | [[Category:ММ РУиС (дисциплина)]] | ||
Версия 14:34, 21 августа 2013
При моделировании следящих систем НАП, а так же сигналов многоантенных НАП, возникает задача создания нормальных случайных величин с заданным коэффициентом корреляции.
Многомерная нормальная СВ или вектор случайных величин?
При синтезе радиотехнических систем часто используются модели, оперирующие с многомерными нормальными распределениями.
Определение из Википедии:
Случайный вектор  имеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных условий:
имеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных условий:
- Произвольная линейная комбинация компонентов вектора
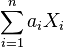 имеет нормальное распределение или является константой.
имеет нормальное распределение или является константой.
- Существует вектор независимых стандартных нормальных случайных величин
 , вещественный вектор
, вещественный вектор 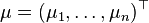 и матрица
и матрица 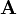 размерности
размерности  , такие что:
, такие что:
-
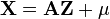 .
.
- Существует вектор
 и неотрицательно определённая симметричная матрица
и неотрицательно определённая симметричная матрица 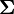 размерности
размерности 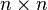 , такие что характеристическая функция вектора
, такие что характеристическая функция вектора 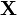 имеет вид:
имеет вид:
-
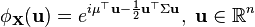 .
.