Требования, предъявляемые к навигационным сигналам (ОП СРНС, лекция)

Навигационные определения формируются в СРНС второго поколения на базе псевдодальномерного метода. Навигационный сигнал должен позволять реализовывать этот метод. Давайте поставим себя на место разработчика навигационной системы. Сигнал какой структуры нам выбрать? Какие требования к нему предъявить?

На качественном уровне, укрупнено, сигнал каждого НС должен:

• Позволять хорошо определять псевдодальность;
• Передавать информацию о положении НС системы;
• Быть отличимым от сигналов других НС;
• Не мешать другим радиосистемам;
• Не требовать для приема и передачи сложной аппаратуры.

Точность определения псевдодальности

Сигнал должен позволять точно восстанавливать кодовое сигнальное время несмотря на действие шумов.

Кодовое сигнальное время определяется по огибающей сигнала - модуляции несущей частоты.

Допустим, используется некоторый сигнал 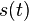$s(t)$. Допустим, на приемной стороне известна его частота, амплитуда, начальная фаза - то есть все параметры, кроме задержки огибающей. Рассмотрим случай, когда сигнал наблюдается на фоне белых некоррелированных гауссовых шумов 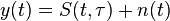$y(t) = S(t, \tau) + n(t)$ на некотором временном интервале длительностью 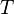$T$. Считается, что задержка на этом интервале не меняется. В статистической теории радиотехнических систем найдена потенциальная граница точности (СКО) оценки задержки 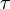$\tau$ такого сигнала по наблюдениями $y(t)$:

$\sigma_{\tau} = \frac{1}{\sqrt{2q}\beta}$,

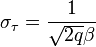где

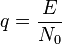$q = \frac{E}{N_0}$ - отношение сигнал/шум,

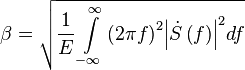$\beta = \sqrt{{\frac{1}{E}\int\limits_{ - \infty }^\infty {{{\left( {2\pi f} \right)}^2}{{\left| {\dot S\left( f \right)} \right|}^2}df} }}$ - эффективная ширина спектра радиосигнала,

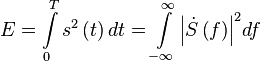$E = \int\limits_0^T {{s^2}\left( t \right)dt} = \int\limits_{ - \infty }^\infty {{{\left| {\dot S\left( f \right)} \right|}^2}df}$ - энергия сигнала за время наблюдения,

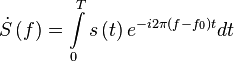$\dot S\left( f \right) = \int\limits_0^T {s\left( t \right){e^{ - i2\pi (f-f_0)t}}dt}$ - спектральная плотность сигнала записанная относительно несущей.

В реальной аппаратуре полоса радиотракта ограничена, поэтому интеграл при расчете следует ограничить в пределах. Кроме того, эта постановка задачи не в полной мере отражает работу приемника - задержка меняется во времени, поэтому используют системы слежения. Тем не менее, эти выражения позволяют установить качественно связь между параметрами сигнала и точностью оценки его задержки (а значит и кодового сигнального времени, псевдозадержки, псевдодальности).

В формуле эффективной ширины спектра присутствует множитель вида 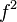$f^2$ - парабола. Следует вывод - по гармоническому колебанию задержку не определить, а для уменьшения ошибки определения задержки следует увеличивать ширину спектра сигнала. В пределе наилучшую точность обеспечивают сигнал с двумя компонентами в спектре, максимально отдаленными от несущей.

Точность определения псевдоскорости

Аналогичные выражения можно найти для потенциальной точности оценки доплеровского смещения частоты:

$\sigma_{\tau} = \frac{1}{\sqrt{2q}\alpha}$,

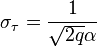где

$\alpha = \sqrt{{\frac{1}{E}\int\limits_0^T {{{\left( {2\pi t} \right)}^2}} {s^2}\left( t \right)dt} }$ - эффективная длительность сигнала.

Передающая аппаратура работает эффективно при использовании сигналов с постоянной огибающей, а для них:

$\alpha = \sqrt{ {\frac{2}{T}\int\limits_0^T {{{\left( {2\pi t} \right)}^2}} {{\cos }^2}\left( {\omega t} \right)dt} } \approx 3,628T$,

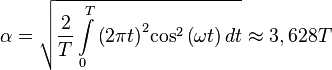откуда можно сделать вывод, что их конкретный вид не влияет на точность определения доплеровского сдвига, а значит и псевдоскорости.

Предоставление эфемеридных данных и альманаха

Для передачи эфемеридной информации можно использовать и другие каналы связи, но удобнее - совмещать в навигационном сигнале функции носителя сигнального времени и навигационных данных.